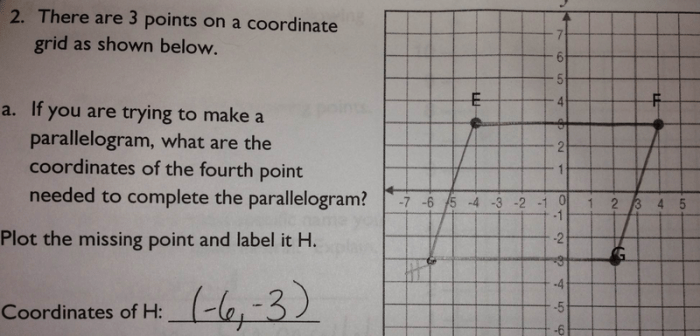Coordinate geometry name that quadrilateral worksheet answers – Embark on an enlightening journey into the realm of coordinate geometry, where the mysteries of quadrilaterals unravel. With this comprehensive guide, we delve into the depths of quadrilateral properties, unlocking the secrets that lie within their geometric intricacies. Prepare to be captivated as we unravel the intricate relationship between coordinates and quadrilaterals, empowering you to conquer any quadrilateral conundrum that may arise.

Through the lens of coordinate geometry, we will decipher the essence of quadrilaterals, unraveling their unique characteristics and unlocking their hidden potential. From the fundamental properties that define them to the intricate relationships between their sides and angles, we will leave no stone unturned in our quest for quadrilateral mastery.

Coordinate Geometry and Quadrilaterals

Coordinate geometry is a branch of mathematics that uses coordinates to represent points and shapes on a plane. It is a powerful tool for solving problems involving quadrilaterals, which are polygons with four sides.

To represent a quadrilateral using coordinate geometry, we need to know the coordinates of its vertices. The vertices of a quadrilateral are the points where its sides intersect. Once we know the coordinates of the vertices, we can use them to find the length of the sides, the area of the quadrilateral, and other properties.

Using Equations to Represent Quadrilaterals, Coordinate geometry name that quadrilateral worksheet answers

We can also use equations to represent the sides and diagonals of a quadrilateral. The equation of a line is a mathematical statement that describes the relationship between the coordinates of the points on the line. We can use the equations of the sides and diagonals of a quadrilateral to find their lengths, slopes, and other properties.

Area and Perimeter of Quadrilaterals

The area of a quadrilateral is the amount of space that it occupies on the plane. The perimeter of a quadrilateral is the sum of the lengths of its sides. We can use the formulas for the area and perimeter of a quadrilateral to solve problems involving these properties.

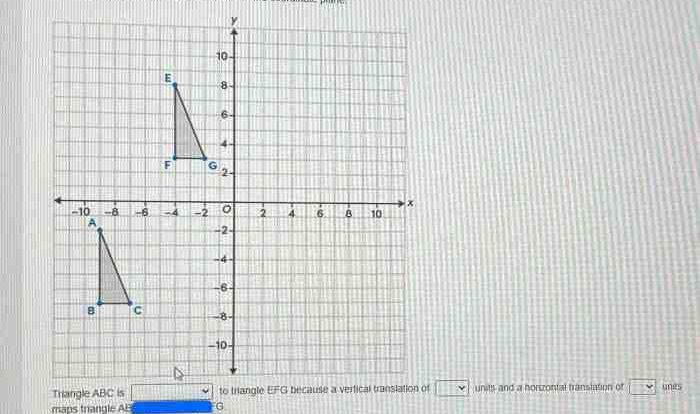
Transformations of Quadrilaterals

Transformations are operations that can be applied to quadrilaterals to change their size, shape, or orientation. The most common transformations are translations, rotations, and reflections. We can use coordinate geometry to perform these transformations on quadrilaterals.

Applications of Coordinate Geometry in Quadrilateral Problems

Coordinate geometry is used in a wide variety of applications, including design, engineering, and computer graphics. For example, coordinate geometry can be used to design buildings, bridges, and other structures. It can also be used to create animations and special effects in movies and video games.

FAQs: Coordinate Geometry Name That Quadrilateral Worksheet Answers

What is the relationship between the coordinates of a quadrilateral and its properties?

The coordinates of a quadrilateral’s vertices determine its shape, size, and orientation. By analyzing the coordinates, we can determine properties such as side lengths, angles, area, and perimeter.

How can I use coordinate geometry to solve problems involving quadrilaterals?

Coordinate geometry provides a powerful tool for solving quadrilateral problems. By representing quadrilaterals as points and lines on a coordinate plane, we can use algebraic equations and geometric relationships to determine their properties and solve problems related to their area, perimeter, and transformations.

What are some real-world applications of coordinate geometry in relation to quadrilaterals?

Coordinate geometry finds applications in various fields, including architecture, engineering, and computer graphics. For example, architects use coordinate geometry to design buildings and structures, while engineers use it to analyze forces and stresses in bridges and other structures.